Dr. Arnulf Schönlieb

Paul Puntigam und sein Bier – eine Einführung in die Differentialrechnung

Paul Puntigam trinkt gern Bier, aber er mag den Schaum nicht. Bei seinem letzten Wirtshausbesuch hat er festgestellt, dass ein liebevoll gezapftes Bier beim Servieren eine Schaumkrone von 5cm aufweist. Mit dem Trinken musste Paul insgesamt 4 Minuten warten. Erst dann war die Schaumkrone auf  ¹/₂ cm gesunken und er konnte den ersten Schluck genießen.

Wenn man annimmt, dass sich die Abnahme des Schaums im Bierglas nicht linear vollzieht, kann man die Schaumhöhe zum Zeitpunkt t als Funktion S(t)= at² + b mit a, bÎÂ veranschaulichen.

a)      Bestimme die Gleichung der Schaumhöhenfunktion!

Wenn man zum Zeitpunkt t=0 von der bekannten Schaumhöhe 5cm  ausgeht, folgt unmittelbar b=5. Wegen S(4) = ¹/₂ kann man 16a + b = ¹/₂ setzen. Aus dieser Gleichung berechnet man 16a = - ⁹/₂ und folglich a=- ⁹/₃₂. Pauls Schaumfunktion lautet somit:

S(t) = -⁹/₃₂t² + 5. Ihr Verlauf ist in der nebenstehenden Graphik dargestellt:

b)      Wann ist der gesamte Schaum verschwunden?

 

Diese Frage lässt sich leicht beantworten. Man bestimmt dazu den  Zeitpunkt t₁ mit S(t₁) = 0, genaugenommen die Nullstelle der Funktion. Nach kurzer Rechung erhält man t₁= 4,22 Minuten.

c)      Wie schnell sinkt die Schaumhöhe pro Minute?

Hier ist es schon schwieriger, eine eindeutige Antwort zu geben. Es ist offensichtlich, dass die Höhe des Schaums mit zunehmender Dauer immer  rascher abnimmt. Einfache Berechnungen für die Zeitintervalle [0; 1], [1; 2], [2; 3], [3; 4] bestätigen dies. Man erhält:

Intervall	[0; 1]	[1; 2]	[2; 3]	[3; 4]
Abnahme in cm	- 9/32cm	- 27/32cm	- 45/32cm	- 63/32cm

Wählt man nicht von vornherein ganze Minutenintervalle, sondern interessiert sich beispielsweise für die mittlere Abnahme des Schaums pro Minute im Zeitraum [2; 3,5], so kann man folgend überlegen: Man erhält einen brauchbaren Wert für die mittlere Abnahme pro Minute, wenn man die im jeweiligen Zeitraum erfolgte Schaumabnahme auf genau diesen Zeitraum bezieht. Für das Intervall [2; 3,5] heißt das:

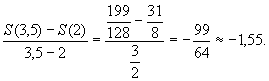
Im angegebenen Zeitraum sinkt die Schaumhöhe somit um 1,55cm pro Minute. Allgemein kann man die Berechnung der mittleren Änderung der Schaumhöhe folgend beschreiben: Die mittlere Änderungsrate der Schaumhöhe im Zeitintervall [t₀, t] berechnet man aus: _. Man nennt diese Größe den Differenzenquotienten der Funktion S(t) im Intervall [t₀. t].

Beispiel 1: Bei alkoholfreiem Bier der Marke „Clausthaler Herbfrisch“ fällt auf, dass die Schaumhöhe zu Beginn zwar größer ist, der Schaum jedoch wesentlich rascher in sich zusammenfällt. Schenkt man ein Glas Clausthaler voll, steht der Schaum im allgemeinen etwa 7cm hoch im Glas, nach etwa 2 Minuten ist die Schaumhöhe aber schon auf 1cm zurückgegangen.

a)      Stelle unter der Annahme einer Funktion S₁(t) = at² + b die Gleichung der Schaumhöhenfunktion für „Clausthaler“ auf und zeichne sie! [S₁(t)=-³/₂t² + 7]

b)      Wie hoch steht der Schaum nach 1,5 (3) Minuten? [²⁹/₈ cm bzw. –6,5cm!!, kein Schaum mehr!]

c)      Wann ist überhaupt kein Schaum mehr vorhanden? [nach  2,16 Minuten!]

d)      Wie rasch nimmt der Schaum in den Zeitintervallen [1; 1,4], [0,5; 2], [1,5; 1,55] pro Minute ab? Berechne die mittlere Abnahmegeschwindigkeit  für die angegebenen  Intervalle! [-3,6cm bzw. –3,75cm bzw. –4,575cm]

Die nebenstehende Graphik veranschaulicht beide Funktionen in einem Koordinatensystem und lässt einige interessante Zusammenhänge herausarbeiten. Beispielsweise kann man unmittelbar aus der Darstellung entnehmen, wann beide Gläser dieselbe Schaumhöhe aufweisen. Dieser Zeitpunkt lässt sich unmittelbar durch Gleichsetzen der „Bierschaumfunktion“ S(t) und der „Clausthalerschaumfunktion“ S₁(t) berechnen. Man erhält t=1,281 Minuten.

Komplizierter wird es, wenn man die „Geschwindigkeit“ der Schaumabnahme für beide Funktionen näher untersuchen und Vergleiche anstellen möchte. Wie kann man etwa die Abnahmegeschwindigkeit des Bierschaums zu einem beliebigen Zeitpunkt, etwa zum Zeitpunkt t=2, ermitteln?

Wir betrachten dazu nochmals Pauls Schaumfunktion: S(t) = -⁹/₃₂t² + 5.

Für die Schaumabnahme im Zeitintervall [2; 3] gilt:

Eine geometrische Interpretation der durchschnittlichen Schaumabnahme ist recht einleuchtend. Wir haben ja gerade den durchschnittlichen Anstieg einer Funktion berechnet, die durch die beiden Punkte P(t₀, S(t₀)) und Q(t, S(t)) geht. Die Gleichung dieser linearen Funktion können wir leicht bestimmen. Für die lineare Funktion g(t) = kt+d gilt:

k= _. Die Konstante d kann man durch Einsetzen eines der beiden Punkten P oder Q unmittelbar berechnen. Für das Intervall [2; 3] erhält man etwa:

k= -1,40625. Für P und Q erhält man: P(2; 3,875) bzw. Q(3; 2,46875). Daraus bestimmt man:

d = 1,40625 ∙ 2 + 3,875 = 6,6875.

Die Gleichung der Geraden g lautet somit: g(t) = -1,40625 ∙ t +6,6875. Zeichnet man die Funktion S(t) sowie die Gerade g(t) in ein Koordinatensystem, erkennt man, dass g(t) die Funktion S(t) gerade in den beiden Punkten P und Q schneidet und eine Sekante dieser Funktion ist.

Wir können nun versuchen, die Schaumabnahme zum Zeitpunkt t=2 zu bestimmen, indem wir das Intervall schrittweise verkleinern. Einen besseren Näherungswert für den "Anstieg" (hier Abnahme) der Funktion zum Zeitpunkt t=2 erhält man, wenn man beispielsweise das Intervall [2; 2,5] wählt. Es ergibt sich für die Schaumabnahme  _. Durch weitere Verfeinerung des Intervalls erhält man:

Man erkennt, dass die Werte der durchschnittlichen Änderung einem bestimmten Wert zuzustreben scheinen. Dieser Wert lässt sich allerdings nicht direkt ermitteln, da der Term  für t=t₀ nicht definiert ist. Daher ist es nicht möglich, in der obigen „Formel“ einfach t=2 zu setzen. Wir sehen aber, dass wir für Werte von t, die sehr nahe bei 2 liegen, nur noch geringe Unterschiede in den Ergebnissen erhalten. Man kann nun diese Berechnung weiter vereinfachen, indem man die Formel folgendermaßen umformt:

Mit dieser Formel findet man recht schnell brauchbare Näherungswerte für die durchschnittliche Schaumabnahme zum Zeitpunkt t=2, insbesondere dann, wenn t sehr nahe bei 2 ist. Dass wir nicht einfach t=2 setzen dürfen, haben wir schon festgestellt. Wir können aber folgend überlegen: Nähert sich t unbegrenzt der Zahl 2, so nähert sich der Term unbegrenzt der Zahl =-1,125. Wir formulieren dazu:

Ist es Zufall, oder lässt sich der obige Umformungsschritt bei jedem Beispiel anwenden und damit verallgemeinern.

Nun , es ist so, dass für Funktionen der Form f(x) = ax² + b dieser „Zerlegungstrick“ tatsächlich immer zum Erfolg führt. Wir werden auch sehen, dass dies für Polynomfunktionen ganz allgemein gilt. Für Funktionen anderer Typen werden wir uns aber (zwangsläufig) weitere Methoden überlegen müssen.

Für die Funktion S(t) kann man die Zerlegung allgemein folgend durchführen:

Auch im Falle der momentanen Schaumabnahme kann man eine geometrische Interpretation angeben. Die Veränderung bei t=2 entspricht ja genaugenommen der Steigung der Funktion S(t) in t=2. Dementsprechend muss es auch hier eine Gerade h(t)=kx + d geben, die die Funktion im Punkt T(t₀, S(t₀)) berührt, also Tangente an S(t) im Punkt T ist. Für die Gleichung dieser Funktion berechnet man in gleicher Weise wie oben h(t)= 1,125 ∙t + 6,125.

Zeichnet man diese Gerade gemeinsam mit der Funktion in ein Koordinatensystem, ergibt sich nebenstehendes Bild:

Wir können unsere Überlegungen damit folgend zusammenfassen:

Die durchschnittliche Änderungsrate entspricht der Steigung der Sekante durch die beiden Intervallendpunkte. Man nennt den Differenzenquotient von S(t) im Intervall [t₀, t].

Die momentane Änderungsrate an einer Stelle t=t₀ entspricht der Steigung der Tangente im Punkt T(t₀, S(t₀)).

Man nennt den Differentialquotient von S(t) im Punkt t=t₀. Der Differentialquotient S’(t₀) wird meist als erste Ableitung der Funktion S(t) bezeichnet. Den Vorgang bei der Bildung des Differentialquotienten nennt man ableiten oder differenzieren.

Für Funktionen der Form f(x)= ax² + b kann man zur Bildung von f ’(x₀) folgende Regel angeben:

Übungen:

1)      Bestimme für die Funktion f(x) = 3x² + 1 nach dem obigen Muster die Gleichung der Tangente im Punkt P(1, y) der Funktion. [t: y=6x-2]

2)      Bestimme für die Funktion g(x) = x² +9 die Gleichungen der Tangenten in den Punkten P(-2, y) und Q(2, y)!

Wodurch unterscheiden sich die beiden Tangentengleichungen? [t_P: y=-4x+5, t_Q : y=4x+5, siehe Skizze]

Wie kann man nun allgemein den Differentialquotienten einer Potenzfunktion f(x) = xⁿ berechnen.

Wir gehen dabei in der gleichen Weise vor wie im vorhergehenden Beispiel und greifen auf eine bekannte binomische Zerlegungsformel allgemeiner Art zurück.

Es gilt nämlich:

Man nennt diese Formel Potenzregel für ganzzahlige Exponenten, da, wie wir sehen werden, auch Potenzfunktionen mit negativen ganzzahligen Exponenten bequem differenziert werden können.

Bereits bei der Ableitung der Funktion f(x) = ax² + b haben wir bemerkt, dass die additive Konstante b beim Differenzieren aufgrund der Differenzbildung wegfällt. Die multiplikative Konstante a hingegen bleibt erhalten, wird jedoch beim Differenzieren nicht berücksichtigt.

Wir formulieren folgende Regeln:

Konstantenregel für additive Konstanten:

Es gilt: f(x) = c             f ’(x) = 0

Konstantenregel für multiplikative Konstanten:

Es gilt: für:

g(x) = a ·  f(x)                          g ’(x) = a · f ’(x)

Übungen:

1) In ein 16cm hohes Glas, in dem sich 3cm hoch Orangensaft befindet, wird aus einer Flasche Saft solange dazugegossen, bis das Glas bis 1cm unter den oberen Rand gefüllt ist.

Die jeweilige Füllhöhe lässt sich in Abhängigkeit von der Zeit durch die Funktion

f(t) = 0.6t² + 3 beschreiben.

a)      Bestimme die Änderung der Füllhöhe für drei beliebige Zeitintervalle!

b)      Wann ist das Glas gefüllt (1cm unter dem oberen Rand)? Wie lange dauert der gesamte Füllvorgang? (ca. 4,47 Sekunden)

c)      Bestimme die „Füllgeschwindigkeit nach 2 Sekunden (4 Sekunden)! [2,4 bzw 4,8cm je Sekunde)

d)      Wenn man annimmt, dass das Glas zylinderförmig mit einem Durchmesser von 6cm ist, welchen „momentanen“ Flüssigkeitszuwachs hat man dann zum Zeitpunkt t=2? (Anleitung: Bestimme dazu ausgehend von der Füllhöhenfunktion eine „Volumsfunktion“ nach der bekannten Volumsformel für Zylinder!) Du erhältst:

V(t) =  und daraus V ’(2) = cm³ je Sekunde.

e)      Skizziere den Verlauf der Füllfunktion sowie der Volumsfunktion!

 

 

 

 

 

 

 

 

 

 

 

 

2) Das durchhängende Seil einer Materialseilbahn lässt sich ungefähr durch den Verlauf der Funktion f(x) = ¹/₅₀ · (x-10)² + 100 beschreiben. Ist das Seil an der Stelle x=20 oder an der Stelle x=30 steiler? Bestimme auch die Gleichungen der jeweiligen Tangenten!

[bei x=20 ist k=0,4, bei x=30 ist k=0,8, t bei x=20: y= ²/₅ x + 94, t bei x=30: y= ⁴/₅ x + 84, siehe Skizze:

 

 

3) Ein Experte schätzt, dass die Länge (in km ) eines bestimmten Gletschers nach t Jahren durch die Formel L(t)=¹/₂₀₀₀ · (t-140)² angegeben werden kann.

a)      Nach wie vielen Jahren ungefähr wird der Gletscher verschwunden sein? [nach ca. 140 Jahren]

b)      Bestimme die Abnahmegeschwindigkeit nach 20, 40, 60, 80, 100 Jahren! Nimmt deren Betrag zu oder ab? [L’(20) = -0,1, L’(40) = -0,08, L’(60) = -0,06, L’(80) =-0,04, L’(100) = -0,02, nimmt ab!]

4) Für einen Kleinwagen beträgt die Bremsverzögerung a=-4^m/s² .

a) Zeige, dass die Funktion s(t) = v₀ t - 2 t² dieser Verzögerung entspricht! s(t) gibt dabei den Bremsweg in m an.

b) Wie groß ist die Momentangeschwindigkeit des Fahrzeugs bei v₀  =50 km/h (100 km/h) nach 2, 4, 6 Sekunden!

c) In Fahrschulen wird zur Berechnung des Bremsweges die Formel s(v) = v²/100 gelehrt. Vergleiche die Resultate, die man mit dieser Formel erhält, mit den tatsächlichen Werten!

5) Für einen mit der Geschwindigkeit v₀ lotrecht nach oben geworfenen Gegenstand gilt:

s(t) = v₀ · t – 5t²

a)      Bestimme allgemein den höchsten Punkt, den der Gegenstand erreicht! Zu welchem Zeitpunkt erfolgt dies?

b)      Wann prallt der Gegenstand wieder am Boden auf?

Den höchsten Punkt erhält man aus der Überlegung, dass dort  v(t)=0 gelten muss. Man bildet entsprechend s’(t)= v₀ – 10t, setzt die Ableitung Null und berechnet daraus . Die Höhe zu diesem Zeitpunkt erhält man aus s(t) mit und damit: . Den Aufprallzeitpunkt berechnet man aus s(t)=0 mit .

Die nebenstehende Graphik veranschaulicht die Wegfunktionen für v₀=10^m/_s, 15^m/_s, 30^m/_s, 40^m/_s

6) (Fortsetzung von Beispiel 5)

Bei einem Feuerwerk wird eine Rakete mit v₀=32^m/_s senkrecht nach oben geschossen, die an ihrem höchsten Punkt explodiert. Mit welcher Geschwindigkeit müssen zwei weitere Raketen im Abstand von jeweils einer Sekunde später hoch geschossen werden, damit sie die erste Rakete an ihrem höchsten Punkt einholen. Wie hoch steigen die beiden anderen Raketen? Skizziere für alle drei Raketen ihre Flughöhe im Zeitverlauf!

Lösung zu 6)

Für die senkrecht nach oben geschossene erste Rakete gilt: s(t) = v₀ · t – 5 t² mit v₀=32^m/_s.

Für die eine Sekunde später abgefeuerte Rakete gilt entsprechend: s₁(t) = v₁ · (t – 1 ) – 5 (t – 1)². Ebenso gilt für die dritte Rakete: s₂(t) = v₂ · (t – 2 ) – 5 (t – 2)². Aus dem vorhergehenden Beispiel ist klar, dass die maximale Höhe zum Zeitpunkt  erreicht wird und Meter beträgt. Für die eine Sekunde später mit einer Anfangsgeschwindigkeit v₁ gestartete Rakete muss gelten: . Entsprechend muss auch für die dritte Rakete gelten: .

Man erhält daraus die Gleichung: . Aus dieser Gleichung berechnet man . Für die dritte Rakete gilt entsprechend: . Aus dieser Gleichung berechnet man .

Setzt man nun für v₀=32^m/_s ein, erhält man: v₁=34,27^m/_s bzw. v₂=48,66^m/_s.

Die maximale Höhe der beiden nachfolgenden Raketen erhält man aus  und . Die nebenstehende Graphik veranschaulicht die Höhe der drei Raketen zu den jeweiligen Zeitpunkten.

7) Heavy Harry, eine wahrhaft gewichtige Gestalt der New Yorker Unterwelt, fand ein unrühmliches Ende, als er von einer unbekannten Hand aus einem Fenster des 65. Stockwerks gestoßen wurde. Unter der Annahme, das dies einer Höhe von 200m entspricht, lässt sich die Höhe H, in der sich Harry nach t Sekunden befand, durch die Funktion H(t) = 200 – 5t² beschreiben.

a)      Skizziere den Verlauf der Funktion in einem sinnvollen Bereich  und beschreibe alle ihre Eigenschaften!

b)      Wie lange dauerte der „Flug“ Harrys und wie lässt sich dieser Wert interpretieren?

c)      Stelle eine Formel für die mittlere Änderung der Höhe im Zeitraum [t₁, t₂] auf und berechne damit die mittlere Änderung der Höhe pro Sekunde in den Zeitintervallen

[1; 3] und [2; 5]! Interpretiere das Ergebnis!

d)      Mit welcher Geschwindigkeit schlug Harry auf dem Boden auf (vernachlässige den Luftwiderstand!)

 

Differentialrechnung - Fortsetzung: Untersuchen von Funktionsgraphen

Es ist bekannt, dass Umweltkatastrophen (beispielsweise Unfälle mit Tankschiffen) nachhaltige negative Auswirkungen auf das Ökosystem in den betroffenen Regionen haben. Beispielsweise lässt sich beobachten, dass sich eine bestimmte Tierpopulation, die durch ein derartiges Ereignis innerhalb kurzer Zeit stark dezimiert wird, unter bestimmten Voraussetzungen relativ rasch wieder erholen kann. Tritt allerdings innerhalb dieser Erholungsphase eine weitere Katastrophe als Folgeereignis ein, stirbt die Population innerhalb kürzester Zeit aus.

Etwas vereinfacht kann man die Entwicklung der Population unter den genannten Bedingungen recht gut durch eine Kurve dritten Grades veranschaulichen. Wir wollen uns im folgenden Beispiel mit einigen, nicht nur für Ökologen und Biologen interessanten Fragestellungen beschäftigen.

An einem aus ökologische Sicht „gesunden“ Strandabschnitt beobachtete man aufgrund der letzten Vogelzählungen ca. 9000 Seeschwalben. Kurze Zeit später stießen in Strandnähe ein Tankschiff und ein Frachter derart unglücklich zusammen, was zur Folge hatte, dass ein Großteil des Strandes mit Öl verseucht wurde. Beobachtungen im nächsten Jahr ergaben, dass die Seeschwalbenpopulation um 4000 Stück auf etwa 5000 Seeschwalben zurückgegangen war. Ein Teil der Tiere war verendet, einige hatten noch aufs offene Meer flüchten können, in jedem Fall war die Mehrheit der Gelege zerstört worden. Erstaunlicherweise beobachteten Ornithologen (Vogelkundler) bereits nach etwa 3 Jahren, dass sich die Population wieder auf den alten Wert von 9000 Stück eingependelt. Eine kurz danach durch einen Chemieunfall hervorgerufene neuerliche Verunreinigung des Wasser konnte die Population jedoch (vermutlich aufgrund fehlender Widerstandfähigkeit) nicht mehr überstehen. Bereits nach etwa 4 ¹/₂ Jahren konnte man am betreffenden Strandabschnitt keine einzige Seeschwalbe mehr beobachten.

Vereinfacht man die Situation etwas, lässt sich der beschriebene Sachverhalt durch die Funktion P(t) = -1000·(t³ – 6t² + 9t – 9) recht gut beschreiben.

Skizziere den Verlauf der Funktion und interpretiere!

Mit Hilfe einer einfachen Wertetabelle erhält man für den Verlauf der Funktion folgende Darstellung:

Anhand der Zeichnung erkennt man, dass die Populationsfunktion im Intervall [1; 3] streng monoton wachsend, in den Intervallen [0;1] und [1; 4] und darüber hinaus streng monoton fallend ist.

Ziemlich einleuchtend ist außerdem, dass sich der Rückgang der Population nach dem ersten Unglück mit der Zeit langsamer vollzieht während der Rückgang nach dem zweiten Unglück dramatisch zunimmt (die Kurve fällt nach dem zweiten Unglück wesentlich steiler ab!).

Was kann man über die Änderungsraten der Population in bestimmten Zeitintervallen bzw. zu bestimmten Zeitpunkten aussagen?

In jedem Fall gilt, dass die Änderungsrate der Population im Intervall [1; 3] positiv ist (die Population nimmt in diesem Zeitraum ja zu), in den Intervallen [0; 1] und [3; 4] und darüber hinaus negativ ist. Da wir aber die Änderungsrate zu einem bestimmten Zeitpunkt gerade als erste Ableitung erklärt haben, folgt daraus (zumindest anschaulich):

P(t) ist gerade in jenen Zeitintervallen (in jenen Zeitpunkten) streng monoton fallend, in denen P’(t)<0 ist. Ebenso ist P(t) gerade in jenen Zeitintervallen (in jenen Zeitpunkten) streng monoton steigend, in denen P’(t)>0 gilt.

Wir wollen diesen anschaulich klaren Sachverhalt anhand der Funktion P(t) überprüfen.

Dazu bestimmen wir jene Bereiche, in denen P’(t)>0 bzw. P’(t)<0 gilt.

Für P’(t) erhalten wir:

P’(t)= -3000·(x² – 4x + 3) = -3000·(x-1)·(x-3).

Damit kann man folgend überlegen.

Ist x<1, gilt x-1<0 und x-3<0.  Daraus folgt: P’(t)<0.

Ist 1<x<3, gilt x-1>0 und x-3<0.  Daraus folgt: P’(t)>0.

Ist x>1, gilt x-1>0 und x-3>0.  Daraus folgt: P’(t)<0.

Damit ergibt sich das gewünschte Bild. P(t) ist im Intervall [1; 3] streng monoton steigend, in den beiden anderen Intervallen streng monoton fallend.

Wir können den eben hergeleiteten Zusammenhang als Satz formulieren:

Übung: In welchen Bereichen sind die folgenden Funktionen streng monoton steigend bzw. fallend? Zeichne aufgrund dieser Ergebnisse und mit Hilfe einiger weiterer Funktionswerte die Funktionen!

a) f(x) = - ¹/₉ · (4x² + 8x + 13)      b) f(x) = - ^¾ · (x² – 3x)

c) f(x) = ¹/₃ · (x³ – 6x² + 9x – 4)    d) f(x) = ¹/₆ ·(2x³ + 3x² – 12x + 14)

[a) str.m.st. in (-∞, -1], str.m.f. in [1, ∞), b) str.m.st. in (-∞, -2], str.m.f. in [2, ∞),

c)      str.m.st. in (-∞, 1] und  [3, ∞), str.m.f. in [1, 3], d) str.m.st. in (-∞, -2] und  [1, ∞), str.m.f. in [-2, 1]

Was lässt sich über jene Zeitpunkte aussagen, an denen die Funktion P(t) ihre Monotonie ändert? (Es sind dies die Zeitpunkte t=1 und t=3)

Aus der Zeichnung erkennen wir: P(t) hat an diesen Stellen ihren „größten“ bzw. „kleinsten“ Wert. Größter Wert soll dabei nicht heißen, dass es nicht einen Zeitpunkt geben kann, an dem die Population einen noch größeren Wert annimmt, aber innerhalb einer bestimmten Umgebung (von t=3) nimmt die Funktion keine größeren Werte an. Wir bezeichnen eine solche Stelle als lokale Maximum bzw. Minimumstelle.

Anschaulich ist klar, dass P(t) bei t=1 ein lokales Minimum und bei t=3 ein lokales Maximum aufweist.

Wir können die gesuchten Zeitpunkte leicht aufgrund der berechneten Monotoniebereiche bestimmen. Wie wir gesehen haben, ändert die Funktion P(t) gerade in den lokalen Extremstellen ihr Vorzeichen, hat aber sonst über das gesamte betrachtete Monotonieintervall dasselbe Vorzeichen. Wir können daher die lokalen Extremstellen (d.h. lokales Maximum bzw. lokales Minimum)der Funktion P(t) sehr leicht aus den Nullstellen der ersten Ableitung P’(t) berechnen.

Setzt man P’(t) = -3000·(x-1)·(x-3)=0, erhält man unmittelbar t=1 bzw. t=3. Ob es sich nun um ein lokales Minimum bzw. Maximum handelt, kann man aufgrund der vorliegenden Monotoniebereiche leicht entscheiden.

Für die Seeschwalbenpopulation berechnet man somit eine Minimalpopulation von P(1) = 5000 Stück, nach 3 Jahren beträgt die Population wieder P(3) =9000 Stück.