Dr. Arnulf Schönlieb

Logistisches Wachstum in der Praxis

Für Wachstumsprozesse, die nach dem logistischen Wachstumsmodell ablaufen, gilt:

(1)

Darin sind p(t) bzw. p₀ die Populationen zu den Zeitpunkten t bzw. t₀, a und b sind die sogenannten Vitalkoeffizienten.

Die Schwierigkeit bei der Modellierung liegt in der Regel darin, die Vitalkoeffizienten a und b zu berechnen. Meist liegen jedoch einige bekannte Werte vor, die die Entwicklung der Population beschreiben helfen. Kennt man die Anfangspopulation p₀ sowie die Größe der Population zu zwei weiteren Zeitpunkten t₁ und t₂, die gleich lange Zeiträume umfassen, d.h. t₂ – t₁ = t₁ – t₀ = t, so kann man folgend überlegen:

Bekannt sind p(t₀) = p₀, p(t₁) = p sowie p(t₂) = p₂.

Daher gilt:

(2) und

(3)

Aus (2) berechnet man:

und damit

(4)

Aus (3) berechnet man in gleicher Weise:

(5)

Daraus folgt:

Wegen a¹0 und p₀¹0 kann man durch a bzw. p₀ kürzen.

Daraus ergibt sich:

Ausmultiplizieren ergibt:

und nach Herausheben:

Setzt man nun , erhält man eine quadratische Gleichung in u.

Eine Lösung dieser Gleichung ist u₁=1. Die zweite Lösung erhält man durch Zerlegen in Linearfaktoren. Der Linearfaktor lautet:

Daraus erhält man:

(6) . Die erste Lösung u₁=1 ergibt: und damit wegen a¹0 den Wert t₁=0. Dies entspricht gerade dem Anfangszeitpunkt t₀ mit p(t₀) = p₀.

Für u₂ berechnet man entsprechend . Logarithmieren auf beiden Seiten liefert: -at=ln(u₂) und weiter:

(7) .

Für gegebenes t (entspricht der Länge des Zeitraums t₁ – t₀ kann man somit den Vitalkoeffizienten a berechnen. Den zweiten Koeffizienten b erhält man durch Rückeinsetzen in (3) oder (4).

Das folgende Beispiel veranschaulicht die Bevölkerungsentwicklung Afrikas bei Anwendung des logistischen Modells:

Bevölkerung Afrika

Jahr	1950	1980	2010
Bevölkerung (in Mio.)	220	470	690

Für die Vitalkoeffizienten berechnet man a=0,04236 und b=0,000050188.

Eine Simulation der Bevölkerungsentwicklung im Zeitraum 1950 – 2100 ergibt folgende Ergebnisse:

Jahr	1950	1960	1970	1980	1990	2000	2010	2020	2030	2040	2050	2060	2070	2080	2090	2100
Bevölkerung	220,0	295,4	380,9	470,0	554,9	629,4	690,0	736,4	770,4	794,3	810,8	822,0	829,5	834,5	837,8	840,0

Die folgende Graphik veranschaulicht das logistische Wachstum:

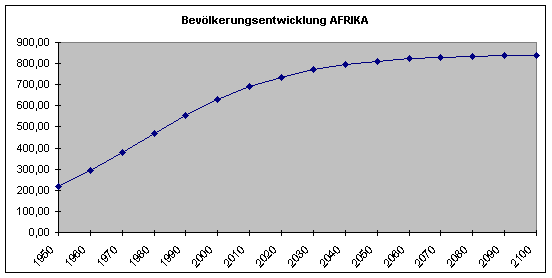
Es ist deutlich erkennbar, dass die jährliche Zuwachsrate etwa bis zum Jahre 1990 noch zunimmt, danach hingegen zurückgeht.

Berechnet man die durchschnittlichen jährlichen Zuwachsraten für den Zeitraum 150 – 2100, so erhält man:

Jahr	1950	1960	1970	1980	1990	2000	2010	2020	2030	2040	2050	2060	2070	2080	2090	2100
Zuwachs	0	7,54	8,55	8,91	8,49	7,45	6,06	4,64	3,39	2,4	1,65	1,12	0,75	0,5	0,33	0,22

Insgesamt nähert sich die Bevölkerung einem Grenzwert, der in diesem Beispiel bei etwa 840 Mio. zu liegen scheint.

Wie kann man nun diesen Grenzprozess beschreiben und den jeweiligen Grenzwert angeben?

Wir berechnen dazu: :

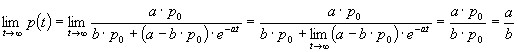Die Grenzpopulation des logistischen Wachstumsmodells ist also .

Nicht in allem Fällen liefert das logistische Wachstumsmodell brauchbare Prognosewerte. Zum einen sind dafür die jeweiligen außermathematischen Rahmenbedingungen verantwortlich, zum anderen gibt es jedoch auch Gründe, die in der Struktur des Modells liegen. Beispielsweise liefert die logistische Modellgleichung (1) nicht immer einen positiven Wert für den Vitalkoeffizienten b. Was dies bedeutet, veranschaulicht die folgende Graphik für a=0,05 und b=-0,000006 bei p₀=220.

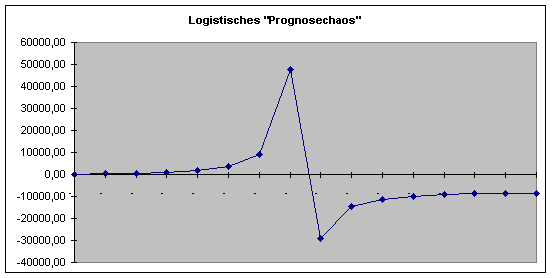
Unter welchen Rahmenbedingungen kann nun eine derartig „chaotische“ Entwicklung auftreten? Wir betrachten dazu nochmals Gleichung (4).

Man erhält für den Vitalkoeffizienten b genau dann einen negativen Wert, wenn gilt:

Nun ist aber " t ÎÂ⁺.

Es genügt daher den Zähler in (4) zu betrachten.

Daraus ergibt sich:

. Wegen p₀¹0 folgt daraus: und weiter:

Damit ist:

und . Formt man den letzten Term schließlich um: , erhält man:

(7) .

Die letzte Aussage kann man folgend zusammenfassen: Ist die Zuwachsrate im Zeitintervall [t₁, t₂] größer als im Zeitintervall [t₀, t₁], gibt es für das logistische Wachstumsmodell keine vernünftige Lösung.

In diesem Fall wird man entweder ein unbeschränktes, exponentielles Wachstum annehmen und dafür entsprechende Modellgleichungen konstruieren oder aber, sofern man genügend Ausgangsdaten hat, andere Beobachtungszeiträume wählen. Die folgenden drei Graphiken veranschaulichen nochmals das „Herantasten“ an den in Ungleichung (7) beschriebenen Zusammenhang. Als Startjahr wird jeweils 1910 angenommen.

Szenario A:

p(t₀)	p(t₁)	P(t₂)	a	b
330	570	960	0,019411	0,000000271231

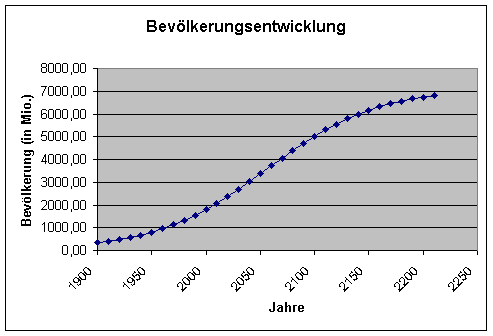
Szenario B:

p(t₀)	p(t₁)	P(t₂)	a	b
330	570	984,54	0,01821837	0,0000000000578

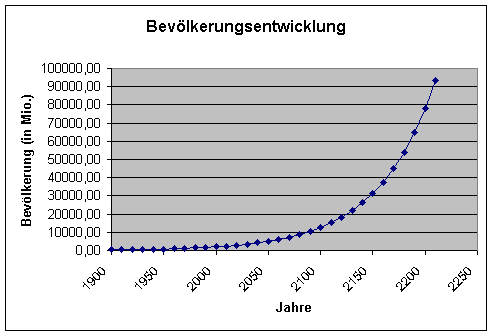
Szenario C:

p(t₀)	p(t₁)	P(t₂)	a	b
330	570	984,545	0,018218145	0,00000000000481