5. Schularbeit - computerunterstützt
7C 19.5.2004
1) Dieses Beispiel ist vollständig und ohne Computerunterstützung im Heft zu rechnen!
a) Eine Ellipse hat die Gerade g: x+4y=9 als Tangente im Punkt T(1, y). Bestimme die Gleichung der Ellipse sowie ihre Brennpunkte!
b)
Gegeben sind die beiden
Hyperbeln hyp1: x2 - y2 = 60 und hyp2:
x2 -8y2 = 32. Berechne die Schnittpunkte der beiden
Kurven, die Gleichungen der Tangenten in einem Schnittpunkt sowie den Schnittwinkel!
2) Die Hyperbel hyp: 3x2 -y2 = 48 wird im Punkt S(8, y >0) von einer Parabel in 1. Hauptlage (y2=2px) geschnitten.
a) Wie lautet die Gleichung dieser Parabel? Bestimme die Brennpunkte für Hyperbel und Parabel!
b) Bestimme die Gleichungen der Tangenten an beide Kurven im Schnittpunkt S!
c) Unter welchem Winkel schneiden einander die Kurven in S?
d) Fertige eine genaue Skizze an (Laptop)! Bestimme dazu die Gleichungen der beiden Hyperbelasymptoten! Stelle beide Kurven, Tangenten sowie Schnittpunkte und Asymptoten in einer Graphik dar!
3) Ein Springbrunnen hat die Form einer ellipsenförmigen Schale, in deren Inneren ein zylinderförmiger Sockel mit der Wasserzuleitung liegt (siehe Skizze). Schale und Sockel sollen gleich hoch sein!
a) Berechne zunächst allgemein, welche Maße der Zylinder haben muss, wenn sein Volumen möglichst groß sein soll! Formuliere exakt die Haupt- und Nebenbedingung! Erkläre die einzelnen Rechenschritte im Heft!
b) Welche Maße hat der Sockel, wenn die Schale eine Durchmesser von 2m und eine Tiefe von 30cm hat?
[1) a) 4P. b) 4P. 2)a) 1P. b) 2P. c)1P. d) 2P. 3) a) 5P. b) 1P.]
Lösungen:
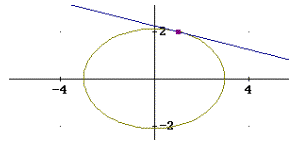
1)a) Durch Einsetzen des Punktes in die Geradengleichung berechnet man: T(1, 2). Die Gerade g hat die Steigung k= -1/4 und d= 9/4.
Da T auf der Ellipse
liegt, gilt: b2 + 4a2 = a2b2.
Ebenso erfüllt die gerade g die Berührbedingung. Es gilt 1/16
a2 + b2 = 81/16 oder a2
+ 16b2 = 81. Setzt man nun für a2 den Term
81-16b2 ein, erhält man: 16b4 – 144b2 + 324=0 und nach Substitution von b2=u für b2 = 9/2.
Für a2 erhält man a2=9. Die Ellipsengleichung lautet daher ell: 9/2 x2 + 9y2 = 81/2 oder
ell: x2 + 2y2 = 9.
Ihre Brennpunkte liegen bei F1(
, 0)
und F2(- 
, 0).
Die nebenstehende Skizze veranschaulicht die Lage von Ellipse, Punkt T und Tangente:
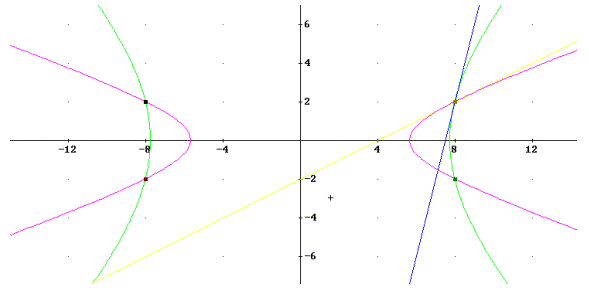
b) Schneidet man die beiden Hyperbeln, erhält man als Schnittpunkte:
S1(8, 2), S2(8, -2), S3(-8, -2), S4(-8, 2). Für hyp1 gilt: a2=b2=60, für hyp2 gilt: a2=32, b2=4. Für die Tangenten an die beiden Hyperbeln im Punkt S1 erhält man:
t1: 480x – 120y = 3600 oder: 4x – y = 30.
t2: 32x – 64y=128 oder : x – 2y = 4.
Für den Schnittwinkel erhält man nach der bekannten Winkelformel für Vektoren: α=49,4°.
Die folgende Skizze veranschaulicht die Situation:
2) a) Durch Einsetzen
des Punktes S in die Hyperbelgleichung erhält man S(8, 12). Die Parabel enthält
den Punkt S und hat daher die Gleichung: y2 = 18x. Für die Hyperbel
gilt: a2 =16 und b2 = 48, für die Parabel p=9. Die Brennpunkte
der Hyperbel lauten entsprechend:
F1(8, 0) und F2(-8, 0), der Brennpunkt der Parabel lautet: F(9/2, 0).
Die entsprechenden Tangenten in S lauten daher: thyp: 384x – 192y = 768 oder
thyp: 2x – y = 4 und tpar: 12y = 9 · (x + 8) oder –3x + 4y = 24. Für den Schnittwinkel berechnet man α=26,56°.
Die Gleichungen der Hyperbelasymptoten lauten: 
.
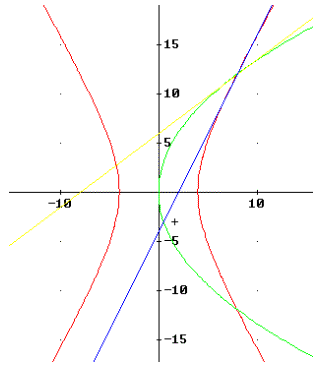Die folgende Skizze veranschaulicht
die Lage der beiden Kurven sowie der Tangenten:
3) a) Skizziert man den Springbrunnen, stellt man fest, dass der Sockel in der Mitte die Form eines Zylinders mit dem Radius x und der Höhe y hat, wenn P(x, y) der gemeinsame Punkt auf der Ellipse ist.
Entsprechend lautet die Hauptbedingung:
V(x, y) = π · x2 · y. Als Nebenbedingung verwendet man die Gleichung der Ellipse.
Man löst nun die Gleichung der Ellipse nach x2 auf und setzt diesen Term in die Hauptbedingung ein. Dies ergibt:
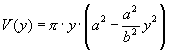. Leitet man diesen Term nach y ab, erhält man :
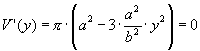. Daraus
ergibt sich 
. Für
x erhält man entsprechend: 
.
b) Für die konkreten Maße des Sockels ergeben sich bei a=100cm und b=30cm:
x=81,64cm und y=17,32cm.