4. Schularbeit - computerunterstützt

7C                                                                                                                             24.3.2004

1) Dieses Beispiel ist vollständig und ohne Computerunterstützung im Heft zu rechnen!

Gegeben ist der Kreis k: x2 + y2 – 4x – 10y –21 = 0

a)      Bestimme Mittelpunkt und Radius des Kreises k!

b)      Berechne die Schnittpunkte des Kreises k mit der Geraden g: x – y = -3!

c)      Bestimme die Gleichungen der Tangenten t1 und t2 parallel zur Geraden g an den Kreis!

2) Die Gerade g: 2x + y = 18 ist Tangente  im Punkt T(8, y) an einen Kreis k, der seinen Mittelpunkt auf der x- Achse hat.

a)      Bestimme aus diesen Angaben die Kreisgleichung! (Skizze!)

b)      Zeige, dass der Punkt Q(6, 4) auf diesem Kreis liegt und bestimme die Gleichung der Kreistangente t in Q!

c)      Zeige, dass die Normale n auf die Kreistangente t im Punkt Q durch den Kreismittelpunkt geht! (Tangenteneigenschaft)

3)

Berechne in der Menge der komplexen Zahlen (ausführlich im Heft!):

a) (1 + 2i)∙ x –2 + i = 4ix – 8i                b)  

4) f(x) = x3 + ax2 + x soll bei x=1 einen Wendepunkt haben.

a)      Bestimme die Funktionsgleichung sowie die Koordinaten des Wendepunktes!

b)      Berechne Lage und Art aller Extremwerte der Funktion!

c)      Skizziere den Verlauf der Funktion möglichst genau!

[1) a)1P. b)3P. c) 2P. 2)a) 2P. b) 2P. c)2P. 3) a) 2P. b) 2P. 4) a)2P. b)2P. c) 2P.]


Lösungen:

1) a) Aus der gegebenen Kreisgleichung berechnet man durch quadratische Ergänzung unmittelbar

k: (x-2)2 + (y-5)2 = 50, woraus sich der Mittelpunkt M(2, 5) und der Radius r= ergibt.

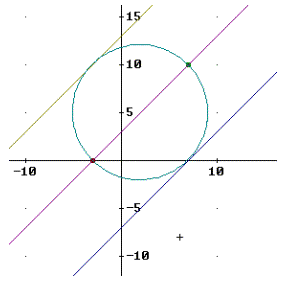Textfeld: b) Die Schnittpunkte des Kreises mit der Geraden g erfolgt durch Einsetzen von g in k. Man erhält folgende quadratische Gleichung: x2 – 4x – 21= 0. Man erhält für die beiden Schnittpunkte S1(7, 10) sowie S2(-3, 0).

c) Die Gleichungen der beiden Tangenten parallel zur Geraden g an den Kreis k bestimmt man mit Hilfe der Berührbedingung. Aus der Gleichung der Geraden g berechnet man k=1 und d=3. Einsetzen in die Berührbedingung: (km – n + d)2 = r2 ∙ (k2 + 1) liefert:

(2-5+d)2 = 100. Daraus berechnet man d1= 13 und d2 = -7. Die beiden Kreistangenten lauten somit:

t1: y = x +13 und t2 : y = x – 7. Die folgende Graphik veranschaulicht die Lage der Schnittpunkte sowie der Kreistangenten :

2) a) Aus der Geraden g berechnet man die Koordinaten des Punktes T als T(8, 2). Da der Kreismittelpunkt auf der x-Achse liegt, erhält man den Mittelpunkt, indem man eine Normale auf g durch den Punkt T legt und mit der x-Achse schneidet. Der Normalvektor dieser Normalen n lautet (-1, 2), ihre Gleichung daher: n: - x + 2y = -4. Schneidet man diese Normale n mit der x-Achse (y=0), erhält man x=4. Der Mittelpunkt des Kreises lautet daher M(4, 0). Den Radius berechnet man aus der Länge des Vektors MT. Man erhält r= .

Die Kreisgleichung lautet: k: (x – 4)2 + y2 = 20.

b) Um zu überprüfen, ob der Punkt Q(6, 4) auf dem Kreis liegt, setzt man ihn einfach in die Kreisgleichung ein! Man erhält unmittelbar eine wahre Aussage! Die Gleichung der Tangente in Q bestimmt man mit Hilfe der Tangentenformel und erhält: t: (x – 4) ∙ 2 + 4y = 20 oder:

t: x + 2y = 14.

c) Die Normale n auf die Kreistangente in Q hat den Normalvektor (-2, 1), ihre Gleichung lautet daher:

n: - 2x + y = -8. Dass der Mittelpunkt M(4, 0) auf dieser Normalen liegt, ist direkt einsichtig !

3) a) (1 + 2i)∙ x –2 + i = 4ix – 8i           

Einfaches Umformen führt auf die Gestalt: (1 - 2i) ∙ x = 2-9i. Die anschließende Division führt auf

x=  4 – i.

b) .

Auch hier führt einfache Multiplikation mit i auf die Gestalt: (1 – 2i) ∙ x = - 4 + 4i. Die anschließende Division führt auf

x=  -12/5 – 4/5 i.

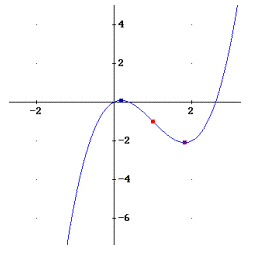
Textfeld:

4) a) f(x) = x3 + ax2 + x hat die zweite Ableitung f ’’(x) = 6x + 2a. Wegen f ’’(1) = 0 gilt a=-3. Die Funktion lautet somit: f(x) = x3 – 3x2 + x. Der Wendepunkt lautet daher W(1, -1).

b) Für f ’(x) berechnet man: f ’(x) = 3x2 -6x + 1 und daraus Punkte mit waagrechter Tangente bei

x1= und x2 = . Daraus erhält man E1(0,1835;0,0886) und E2(1,816, -2,088).

Wegen f ’’(x)<0 in E1 und f ’’(x)>0 in E2 liegt in E1 ein lokales Maximum, in E2 ein lokales Minimum vor! Die folgende Graphik veranschaulicht die Lage der Funktion!