3. Schularbeit 7C / 2003 / 04

Lösungen:

1) a) f(x) = ax⁴ + bx³ hat in W(¹/₃, - ¹/₂₇) einen Wendepunkt. Wegen f ’(x) = 4ax³ + 3bx² und

f ’’(x)=12ax² + 6bx erhält man folgende Bedingungen und Gleichungen:

f (¹/₃) = - ¹/₂₇ und f ’’ (¹/₃) = 0 und damit:

¹/₈₁ a + ¹/₂₇ b = - ¹/₂₇ und ¹²/₉ a + 2b = 0. Das Gleichungssystem hat als Lösung:

a=3 und b=-2.

Die Funktionsgleichung lautet daher f(x)= 3x⁴ – 2x³.

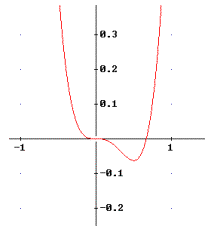
b) Mögliche Extremwerte dieser Funktion erhält man aus: f ’(x)= 12x³ – 6x² = 0. Die Lösungen dieser Gleichung lauten: x₁= x₂=0 , x₃=¹/₂. Wegen f ’’(x) = 36x² – 12x und f ’’ (0) = 0 liegt bei x=0 ein Wendepunkt mit waagrechter Tangente vor (Sattelpunkt). f(x) hat daher nur einen einzigen Extremwert in E(¹/₂, -¹/₁₆). Wegen f ’’(¹/₂)=3>0 ist E lokales Minimum. Die folgende Skizze veranschaulicht den Verlauf der Funktion!

c) f(x) hat einen weiteren Wendepunkt im Koordinatenursprung!

2) Als Hauptbedingung formuliert man:

O(r, h) = 2× r²×π + 2×r× π×h soll minimiert werden unter der Nebenbedingung

r²× π×h = 330.

Aus der Nebenbedingung ermittelt man:

Einsetzen in die Hauptbedingung ergibt:

Man bildet nun die erste Ableitung:

. Daraus berechnet man:

 und damit: r=3,745cm.

Durch Rückeinsetzen in die Nebenbedingung erhält man: h=7,49cm.

Man erkennt, dass h=2r gilt!

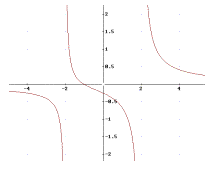
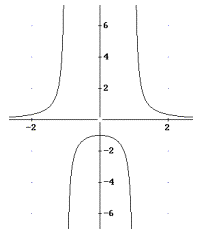
3) a) Die folgenden Graphiken zeigen den Verlauf der Funktionen:

 

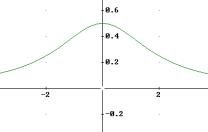b) Die Funktionen f(x) und g(x) weisen Polstellen bei x=± 1 bzw. x=± 2 auf, das an diesen Stellen der Nenner gleich 0 wird. Die Funktion h(x) ist auf ganz R definiert.

c) Die Funktionen f(x) und h(x) weisen eine Symmertrie zur f(x) – Achse auf. Dies ist erkennbar, das f(x) und h(x) nur gerade Hochzahlen enthalten.

d) Bildet man die erste Ableitung, erhält man:

. Man erkennt unmittelbar, dass h(x) bei x=0 eine waagrechte Tangente aufweist. Bildet man die zweite Ableitung, erhält man:

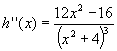. Daher gilt: h’’(0)=-1/4<0. Somit liegt bei P(0, 0) ein lokales Maximum vor.