2. Schularbeit 7C 2003 / 04

Lösungen:

1)      a) f(x) geht durch den Koordinatenursprung, da keine additive Kostante enthalten ist! f(x) kann auch 2 Extremwerte haben!!

b) f(x) = x3 – 3x2 + 5  hat einen zweiten Extremwert (ein lokales Maximum in E1(0, 5)).

c) f(x) = 2x2 + 1 kann nur einen Extremwert haben, da die 1. Ableitung eine lineare Funktion ist.

Textfeld: Wegen f ’’(x)= 4 > 0 kann Extremwert nur ein lokales Minimum sein!

d) f(x) = x3 – x2 hat als zweite Ableitung f ’’(x) = 6x – 2, es gilt daher

f ’’(1)=4 >0, daher linksgekrümmt und nicht rechtsgekrümmt!

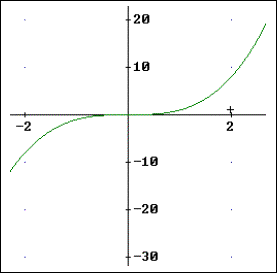
e) f(x) hat bei x=0 Wendepunkt mit waagrechter Tangente (siehe Skizze)

 

 

 

 

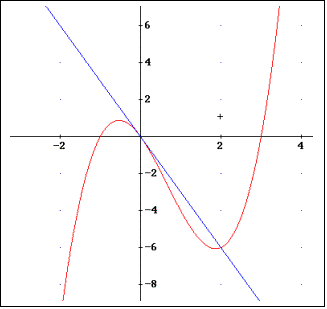
2)      N1(-1, 0), N2(0, 0), N3(3, 0)

Extremwerte bei E1(1,868, -6,06) und E2(-0,535; 0,879)

Wendepunkt bei W(2/3, - 70/27) E2 ist Max, E1 ist Min

Tangente in x=0: y=-3x

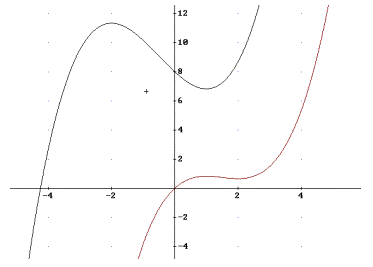Textfeld:

 

 

 

 

 

 

 

 

3)      Textfeld: Gemeinsame Stelle x=1  Extremwert bei E1(1, 41/6) ist Max.  bzw.E2 (1, 5/6) ist Min.