1. Schularbeit 7C 2003 / 04

Lösungen:

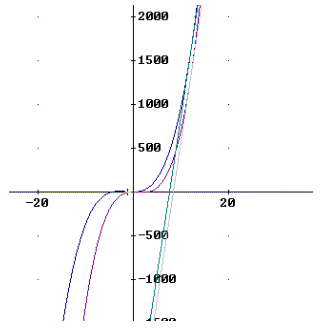
1a) siehe Skizze

b) Nullstelle bei x=8,94 Sekunden.

c) [2; 3]: -25 ^m/_s                        [6; 8] : -70 ^m/_s

d) Ableitung bestimmen: f ’(x) = -10t,d.h. Aufprallgeschwindigkeit=89,4 ^m/_s

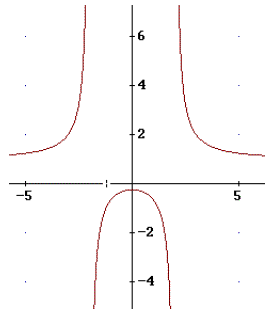
2)

 

 

 

 

 

 

 

 

 

3) a) waagrechte Tangente bei  x=1 bzw. x= -1. P(1, -8) bzw. Q(-1, 8), Max. in Q, Min in P

 

 

 

 

 

 

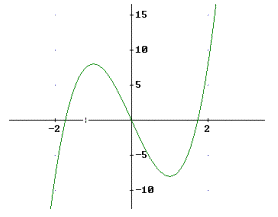
Monotoniebereiche: Dazu f ’ (x) = 12 x² –12 untersuchen. f ’ (x) >0 für x< -1 und x>1, f(x) dort (streng) monoton steigend,  f ’ (x) <0 für x> -1 und x<1, f(x) dort (streng) monoton fallend.

b)

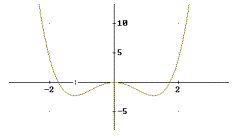f ’(x) = 4x³  - 6x = 0 kann höchstens drei Lösungen haben.

Bei x=0 liegt hier ebenfalls ein Extremwert vor, da sich die Monotonie ändert.

 

 

4) f’ (x) = 3x² – 6x

g’ (x) =2x² + 6x

Daraus erhält man: 3x² – 6x  = 2x² + 6x und damit x₁ = 0 und x₂= 12

d. h. in P₁(0,0) und in Q₁(12, 1296) un Q₂(12,1584)

k_t= 360

daher ist t_f:y=360x+d                       y=360x - 3024

t_g: y=360x + d                                 y=360x  -2736