4. Schularbeit

7A / Gruppe A                                                                                                30.4.2004

1)      Gegeben ist die Kreisgleichung: k: x² + y² – 4x + 6y – 12 = 0

a)      Bestimme Mittelpunkt und Radius des Kreises!

b)      Zeige, dass die Gerade t: 3x + 4y = 19 Tangente an den Kreis k ist! Berechne auch die Koordinaten des Berührpunkts T!

c)      Bestimme die Gleichung einer Ellipse, die durch P(2, -3) geht und den Brennpunkt F( , 0) hat und zeige, dass diese Ellipse genau durch den Kreismittelpunkt geht!

2)      Ein Kreis k hat den Mittelpunkt M(3, 1) und den Radius r= .

a)      Bestimme die Schnittpunkte S₁ und S₂ des Kreises k mit der Geraden g: x – 2y = 1!

b)      Stelle die Gleichungen der Tangenten t₁ und t₂ in den beiden Schnittpunkten auf!

c)      Zeige, dass die Normale n auf die Tangente, die man in einem Schnittpunkt legen kann, durch den Kreismittelpunkt geht!

3)      f(x) = 2x³ + 9x² – 60x

a)      Bestimme für die Funktion f(x) Lage und Art aller Extremwerte und Wendepunkte!

b)      Skizziere den Verlauf der Funktion möglichst genau!

4)      Berechne in der Menge der komplexen Zahlen:

[1) a) 1P. b) 3P. c)2P. 2) a) 4P. b) 1P. c) 1P. 3) a) 4P. b) 2P. 4) 2P.]

4. Schularbeit

7A / Gruppe B                                                                                                30.4.2004

1)      Gegeben ist die Kreisgleichung: k: x² + y² – 6x + 4y – 12 = 0

a)      Bestimme Mittelpunkt und Radius des Kreises!

b)      Zeige, dass die Gerade t: 3x + 4y = 26 Tangente an den Kreis k ist! Berechne auch die Koordinaten des Berührpunkts T!

c)      Bestimme die Gleichung einer Ellipse, die durch P(3, -2) geht und den Brennpunkt F( , 0) hat und zeige, dass diese Ellipse genau durch den Kreismittelpunkt geht!

2)      Ein Kreis k hat den Mittelpunkt M(1, 3) und den Radius r= .

a)      Bestimme die Schnittpunkte S₁ und S₂ des Kreises k mit der Geraden g: -2x + y = 1!

b)      Stelle die Gleichungen der Tangenten t₁ und t₂ in den beiden Schnittpunkten auf!

c)      Zeige, dass die Normale n auf die Tangente, die man in einem Schnittpunkt legen kann, durch den Kreismittelpunkt geht!

3)      f(x) = 2x³ + 9x² – 24x

a)      Bestimme für die Funktion f(x) Lage und Art aller Extremwerte und Wendepunkte!

b)      Skizziere den Verlauf der Funktion möglichst genau!

4)      Berechne in der Menge der komplexen Zahlen:

 

[1) a) 1P. b) 3P. c)2P. 2) a) 4P. b) 1P. c) 1P. 3) a) 4P. b) 2P. 4) 2P.]

Lösungen:

Gruppe A:

1) a) Aus der Kreisgleichung  k: x² + y² – 4x + 6y – 12 = 0 berechnet man durch quadratische Ergänzung unmittelbar : k: (x-2)² + (y+3)² = 25, woraus man M(2, -3) und r=5 ablesen kann.

b) Die Gerade t: 3x + 4y = 19 hat die Steigung k= -³/₄ und d= ¹⁹/₄. Setzt man diese Werte mit r=5 in die Berührbedingung für verschobene Kreise ein, erhält man unmittelbar eine wahre Aussage. Somit ist t Tangente n den Kreis k! Die Koordinaten des Berührpunktes lassen sich rasch ermitteln, indem man eine Normale n auf die Tangente t durch den Kreismittelpunkt legt und mit t schneidet. Da die Normale n den Normalvektor (-4, 3) haben muss, erhält man für sie folgende Gleichung:

n: - 4x + 3y = -17. Löst man nun noch das Gleichungssystem für t und n, erhält man als Berührpunkt T(5, 1).

c) Die Gleichung einer Ellipse mit dem gegebenen Brennpunkt F und P(2, -3) bestimmt man durch Einsetzen in die Ellipsengleichung. Man erhält:

4 b² + 9a² = a²b² sowie a² – b² = 30. Setzt man nun in die erste Gleichung für a² den Term 30+b² ein, erhält man folgende Gleichung: b⁴ + 17b² – 270=0. Setzt man in dieser Gleichung b²=u, erhält man b²=10. Unmittelbar daraus ergibt sich a²=40. Die Gleichung lautet daher: 10x² + 40y² = 400 oder x²+4y²=40. Durch Einsetzen erkennt man sofort, dass der Kreismittelpunkt M(2, -3) auf der Ellipse liegt!

2) a) Aus den Angaben lässt sich die Kreisgleichung unmittelbar formulieren:

k: (x-3)² + (y-1)² = 20. Schneidet man nun den Kreis mit der Geraden g:, erhält man folgende quadratische Gleichung: x² – 6x – 7 =0, woraus man die beiden Lösungen x₁=7 und x₂ = -1 berechnet. Für y₁ und y₂ erhält man y₁=3 und y₂=-1. Die beiden Schnittpunkte lauten somit S₁(7, 3) und S₂(-1, -1).

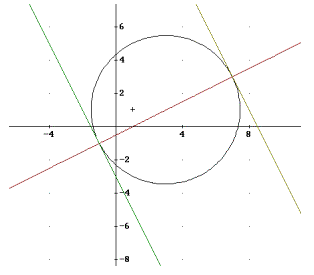
b) Die Gleichungen der Tangenten berechnet man mit der Tangentenformel. Man erhält:

t₁: (x-3) ∙ 4 + (y-1)∙ 2 = 20 oder : t₁: 2x + y = 17 sowie t₂ : (x-3) ∙ (-4) + (y-1)∙ (-2) = 20 oder :

t₂: 2x + y = -3. Die folgende Skizze veranschaulicht die Lage von Kreis und Tangenten:

c) Die Normale n auf t₁ durch S₁ erhält man über den Normalvektor n=(-1, 2). Ihre Gleichung lautet:

n: - x + 2y = -1. Dass der Mittelpunkt M(3, 1) auf dieser Geraden liegt, ist unmittelbar klar.

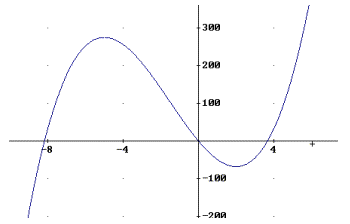
3) f(x) = 2x³ + 9x² – 60x. Man berechnet die erste Ableitung der Funktion  als: f ’(x) = 6x² + 18x – 60.

Für mögliche Extremwerte kommen nur die Nullstellen der ersten Ableitung in Frage. Man erhält:

x₁= -5 und x₂=2. Für die beiden Punkten mit waagrechter Tangente erhält man daher: E₁(-5, 275) und E₂(2, -68). Wegen f ’’(x) = 12x + 18 und f ’’(-5)<0 und f ’’(2)>0 ist E₁ ein lokales Maximum, E₂ ein lokales Minimum. Bei W(-1.5, 103.5) liegt ein Wendepunkt vor. Die nebenstehende Skizze veranschaulicht die Lage der Funktion f(x):

4) a) . Einfaches Erweitern mit dem Nenner ergibt: (1+i)∙x=5. Die anschließende Division ergibt: x= ⁵/₂ – ⁵/₂ i.

Lösungen:

Gruppe B:

1) a) Aus der Kreisgleichung  k: x² + y² – 6x + 4y – 12 = 0 berechnet man durch quadratische Ergänzung unmittelbar : k: (x-3)² + (y+2)² = 25, woraus man M(3, -2) und r=5 ablesen kann.

b) Die Gerade t: 3x + 4y = 26 hat die Steigung k= - ³/₄ und d= ¹³/₂. Setzt man diese Werte mit r=5 in die Berührbedingung für verschobene Kreise ein, erhält man unmittelbar eine wahre Aussage. Somit ist t Tangente n den Kreis k! Die Koordinaten des Berührpunktes lassen sich rasch ermitteln, indem man eine Normale n auf die Tangente t durch den Kreismittelpunkt legt und mit t schneidet. Da die Normale n den Normalvektor (-4, 3) haben muss, erhält man für sie folgende Gleichung:

n:  -4x + 3y = -18. Löst man nun noch das Gleichungssystem für t und n, erhält man als Berührpunkt T(6, 2).

c) Die Gleichung einer Ellipse mit dem gegebenen Brennpunkt F und P(3, -2) bestimmt man durch Einsetzen in die Ellipsengleichung. Man erhält:

9 b² + 4a² = a²b² sowie a² – b² = 14. Setzt man nun in die erste Gleichung für a² den Term 14+b² ein, erhält man folgende Gleichung: b⁴ + b² – 56=0. Setzt man in dieser Gleichung b²=u, erhält man b²=7. Unmittelbar daraus ergibt sich a²=21. Die Gleichung lautet daher: 7x² + 21y² = 147 oder x²+3y²=21. Durch Einsetzen erkennt man sofort, dass der Kreismittelpunkt M(3, -2) auf der Ellipse liegt!

2) a) Aus den Angaben lässt sich die Kreisgleichung unmittelbar formulieren:

k: (x-1)² + (y-3)² = 20. Schneidet man nun den Kreis mit der Geraden g:, erhält man folgende quadratische Gleichung: x² – 2x – 3 =0, woraus man die beiden Lösungen x₁=3 und x₂ = -1 berechnet. Für y₁ und y₂ erhält man y₁=7 und y₂=-1. Die beiden Schnittpunkte lauten somit S₁(3, 7) und S₂(-1, -1).

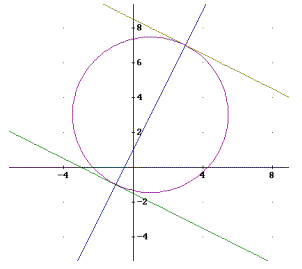
b) Die Gleichungen der Tangenten berechnet man mit der Tangentenformel. Man erhält:

t₁: (x-1) ∙ 2 + (y-3)∙ 4 = 20 oder : t₁: x + 2y = 17

sowie t₂ : (x-1) ∙ (-2) + (y-3)∙ (-4) = 20 oder :

t₂: x + 2y = -3. Die folgende Skizze veranschaulicht die Lage von Kreis und Tangenten:

c) Die Normale n auf t₁ durch S₁ erhält man über den Normalvektor n=(-2, 1). Ihre Gleichung lautet:

n: - 2x + y = 1. Dass der Mittelpunkt M(1, 3) auf dieser Geraden liegt, ist unmittelbar klar.

3) f(x) = 2x³ + 9x² – 24x. Man berechnet die erste Ableitung der Funktion  als: f ’(x) = 6x² + 18x – 24.

Für mögliche Extremwerte kommen nur die Nullstellen der ersten Ableitung in Frage. Man erhält:

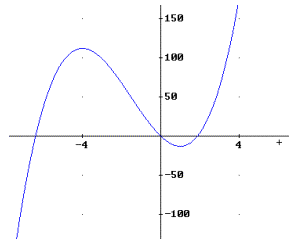x₁= -4 und x₂=1. Für die beiden Punkten mit waagrechter Tangente erhält man daher: E₁(-4, 112) und E₂(1, -13). Wegen f ’’(x) = 12x + 18 und f ’’(-4)<0 und f ’’(1)>0 ist E₁ ein lokales Maximum, E₂ ein lokales Minimum. Bei W(-1.5, 49.5) liegt ein Wendepunkt vor. Die nebenstehende Skizze veranschaulicht die Lage der Funktion f(x):

4) a) . Einfaches Erweitern mit dem Nenner ergibt: (1-i)∙x=-3+4i. Die anschließende Division ergibt: x= -⁷/₂ + ¹/₂ i.