3. Schularbeit 7A 2003 / 04

Lösungen Gruppe A:

1) f(x) = 1/2x2 – x . Durch Einsetzen erhält man unmittelbar P(2, 0).

Für f ’(x) gilt: f ’(x) = x – 1 . f ’(2) = 1. Die ist die Steigung der Tangente in P. Es gilt nun:

g(2) = 0 und g’(2) = 1. Daraus ermittelt man die beiden Bedingungen:

8a + 4b = 0 und 12a + 4b = 1. Die Lösungen des Gleichungssystems lauten: a=1/4 und b=-1/2.

Die Funktion g(x) lautet daher: g(x) =  1/4 x3 - 1/2x2 .

Textfeld: Kurvendiskussion:

g’(x)= 3/4 x2 -x = 0 hat als Lösungen x1=0 und x2= 4/3.

Wegen g’’(x)= 3/2 x -1 und g’’(0)=-1<0 und g’’(4/3)=1>0 hat g(x) in E1(0, 0) ein lokales Maximum und in

E2(4/3, -8/27) ein lokales Minimum.

Wegen g’’(x)= -3/2 x +1=0 folgt x=2/3. g(x) hat in

W(2/3, -4/27) einen Wendepunkt.

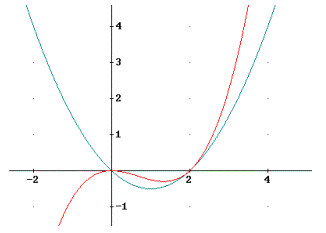
Die folgende Graphik zeigt den Verlauf beider Funktionen:

2)

Der Definitionsbereich dieser Funktion ist R. Es gibt keine Polstellen.

Nullstellen: f(x) hat in N(0, 0) eine Nullstelle:

Für f ’(x) berechnet man:

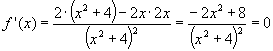
und daraus x1=2 und x2= -2

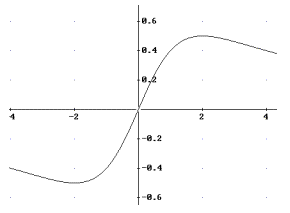Textfeld: Für f ’’(x) berechnet man: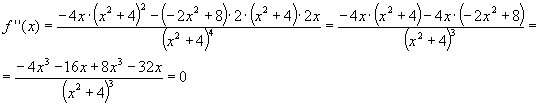

Wegen f ’’(2)<0 liegt bei E(2, 1/2  ) ein lokales Maximum vor.

 

3) Man formuliert als Hauptbedingung:

O(r, h) = 3×r2×π + 2×r× π×h soll minimal werden unter der Nebenbedingung:

V=r2× π×h=1000. Aus der Nebenbedingung berechnet man . Setzt man diesen Term in die Hauptbedingung ein, erhält man:

.

Bildet man die erste Ableitung, erhält man:

.

Daraus erhält man: 6r3×π = 2000 und weiter: =4,734cm. Durch Rückeinsetzen in die Nebenbedingung erhält man: h=14,20cm. Genaugenommen gilt: h=3r.

Lösungen Gruppe B:

1) f(x) = 2x2 – x . Durch Einsetzen erhält man unmittelbar P(2, 6).

Für f ’(x) gilt: f ’(x) = 4x – 1 . f ’(2) = 7. Die ist die Steigung der Tangente in P. Es gilt nun:

g(2) = 6 und g’(2) = 7. Daraus ermittelt man die beiden Bedingungen:

8a + 4b = 6 und 12a + 4b = 7. Die Lösungen des Gleichungssystems lauten: a=1/4 und b=1.

Die Funktion g(x) lautet daher: g(x) = 1/4 x3 +x2 .

Textfeld: Kurvendiskussion:

g’(x)= 3/4 x2 + 2x = 0 hat als Lösungen x1=0 und

x2= -8/3.

Wegen g’’(x)= 3/2 x + 2 und g’’(0)= 2>0 und

g’’(-8/3)=-2<0 hat g(x) in E1(0, 0) ein lokales Minimum und in E2(-8/3, 64/27) ein lokales Maximum.

Wegen g’’(x)= 3/2 x +2=0 folgt x=-4/3. g(x) hat in W(-4/3, 32/27) einen Wendepunkt.

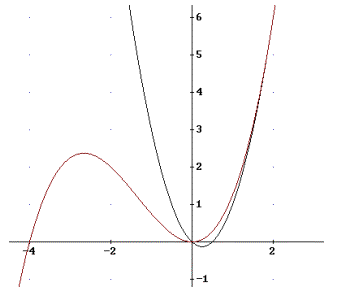
Die folgende Graphik zeigt den Verlauf beider Funktionen:

2)

Der Definitionsbereich dieser Funktion ist R.

Nullstellen: f(x) hat in N(0, 0) eine Nullstelle:

Für f ’(x) berechnet man:

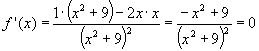
und daraus x1=3 und x2= -3

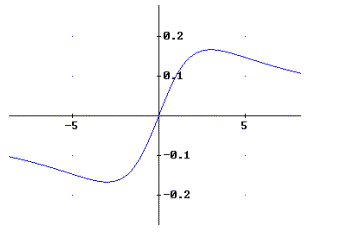Textfeld: Für f ’’(x) berechnet man: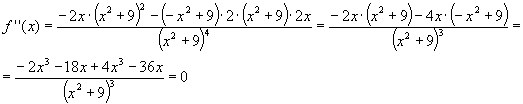

Wegen f ’’(3) <0 liegt in E(3, 1/6 ) ein lokales Maximum vor.

 

3) Man formuliert als Hauptbedingung:

O(r, h) = r2×π + 4×r× π×h soll minimal werden unter der Nebenbedingung:

V=r2× π×h=1000. Aus der Nebenbedingung berechnet man . Setzt man diesen Term in die Hauptbedingung ein, erhält man:

.

Bildet man die erste Ableitung, erhält man:

.

Daraus erhält man: 2r3×π = 4000 und weiter: =8,6cm. Durch Rückeinsetzen in die Nebenbedingung erhält man: h=4,3cm. Genaugenommen gilt: r=2h.