Lösungen Gruppe A:

1) 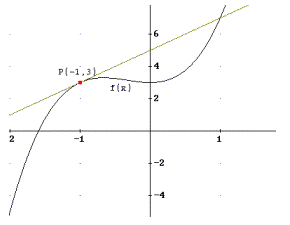     a) f ’(x) = 6x² + 4x , daher k_t= 2 und P(-1, 3), somit t: y=2x+5

 b) Extremwerte bei x=0 und x= - ²/₃

E₁ (0, 3) ist Min, E₂ (-²/₃, ⁸⁹/₂₇) ist Max.

c) Bei x= -¹/₂ und x= -¹/₆.

2)      Wegen P(0, 0) gilt c=0. Aus f(-2) = -2 folgt:

16a - 8b= -2. Aus f ’(-2) = 0 folgt: -32a + 12 b = 0 und daraus a= ³/₈ und b= 1.

b) Waagrechte Tangente bei x=-2 und x=0, d.h.

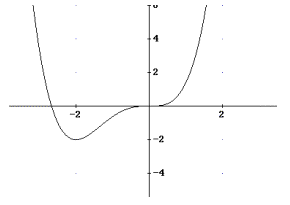E₁(0, 0) und E₂(-2, -2) ,

E₂ ist Min, E₁ ist kein Extremwert! (f ’’(0) =0!!

3)      a) f ’’(x) = 4 >0, daher linksgekrümmt im gesamten Bereich!

b) keine Wendepunkte möglich!

c) f ’(x) ist stets eine quadratische Funktion, hat daher höchstens zwei Lösungen!

d) Erklärung der Änsrungsrate der Tangentensteigung als zweite Ableitung und damit Krümmung der Funktion!

Lösungen Gruppe B:

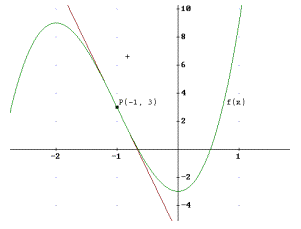1)      a) f ’(x) = 9x² + 18x , daher k_t= -9 und P(-1, 3), somit t: y=-9x – 6.

b) Extremwerte bei x=0 und x= -2 E₁ (0, -3) ist Min, E₂ (-2, 9) ist Max.

c) Bei x= -1.

2)      Wegen P(0, 0) gilt c=0. Aus f(-2) = 2 folgt:

16a – 8b=2. Aus f ’’(-2) = 0 folgt: 48a – 12 b = 0 und daraus a= -¹/₈ und b= -¹/₂.

b) Waagrechte Tangente bei x=-3 und x=0, d.h.

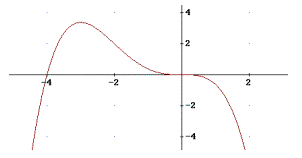E₁(0, 0) und E₂(-3, ²⁷/₈) ,

E₂ ist Max, E₁ ist kein Extremwert! (f ’’(0) =0!!

3)      a) f ’’(x) = -4 <0, daher rechtsgekrümmt im gesamten Bereich!

b) keine Wendepunkte möglich!

c) f ’’(x) ist stets eine lineare Funktion, hat daher genau eine Lösung!

d) Erklärung des Sekanten – Tangenten – Problems!