- Schularbeit
6C 26. 5. 2004
1) Die folgende Tabelle zeigt die Bevölkerungsentwicklung der Stadt Villach (Ergebnisse der VZ 2001):
| 1951 |
1961 |
1971 |
1981 |
1991 |
2001 |
| 43358 |
47140 |
51112 |
52692 |
54640 |
57497 |
a) Erstelle aufgrund der Daten ein Wachstumsmodell der Form Bt=B0 · q t ! Wie groß ist die mittlere jährliche Bevölkerungszunahme in %?
b) Prognostiziere die Bevölkerungszahl für Villach aufgrund dieses Modells für die Jahre 2010 und 2020!
c) In welchem Zeitraum verdoppelt sich die Bevölkerung Villachs nach diesem Modell?
d) In welchem Jahr wird Villach nach dem vorliegenden Modell 70000 Einwohner haben?
2) Aus einem Versandhausangebot: „Kaffeeautomat „Hausfreund“ – 129€. Kaufen Sie jetzt – bezahlen sie in zwei Jahren – zinsenfrei! Bei „Elektromax“ kostet dasselbe Gerät bei Barzahlung 119,90€. Herr Schlau überlegt: Für sein Sparbuch erhält er als guter Kunde 3% Zinsen jährlich.
a) Wo soll er das Gerät kaufen? (Begründung!)
b) Bei welchem Sparbuchzinssatz ist das Versandhausangebot günstiger?
3) Heimo Hitzig, ein hoffnungsvoller Student, hat vor einem Jahr einen Gebrauchtwagen gekauft. Die Hälfte des Kaufpreises von 4000€ zahlte seine Großmutter, für den Rest nahm Heimo einen Bankkredit zu 7% Jahreszinsen auf. Mit der Bank vereinbarte er, den Kredit vierteljährlich mit einer Rate von 200€ zurückzuzahlen.
a) Stelle den Tilgungsplan für die ersten beiden Vierteljahre auf! Rechne dabei mit dem relativen Zinssatz! Erkläre anhand der Tabelle die Bedeutung des Tilgungsanteils!
b) Wann ist der Kredit zurückgezahlt?
c) Berechne die Restschuld nach der vorletzten Zahlung und daraus den Gesamtaufwand für den Kredit!
4) Bei der Verabreichung eines Medikaments weiß man aus Erfahrung, dass die Konzentration des Wirkstoffs 6 Stunden nach der Einnahme auf 30% gesunken ist.
a) Erstelle ein Wachstumsmodell der Form Kt= K0 · e – at ! Wieviel % werden pro Stunde abgebaut?
b) Berechne die Halbwertszeit in diesem Modell und erkläre ihre Bedeutung!
[1) a) 2P. b) 1P. c) 1P. d) 2P. 2) a) 2P. b) 1P. 3) a) 3P. b) 2P. c) 2P. 4)a) 2P. b) 2P.]
Lösungen:
1) a) Aus den vorgegebenen Werten ermittelt man einen relativen Zuwachs von 32,6% im Zeitraum von 50 Jahren. Man erhält entsprechend für den Wachstumsfaktor q=1,00566. Dies entspricht einer jährlichen prozentuellen Zunahme von ca. 0,566%
b) Als Prognosewerte für die Jahre 2010 und 2020 erhält man mit dem genannten Modell:
B2010 = 60493,5 bzw. B2020 = 60493,5 bzw. 64006,5 Einwohner.
c) Die
Verdopplungszeit in diesem Modell erhält man aus der Gleichung: 2· B0
= B0 · q t und damit 
= 122,8
Jahre!
d) Wie
in c) gilt: 70000 = 57497 · q t und daher t=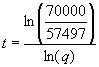 
= 34,86
Jahre, d.h. ca. im Jahre 2036!
2) a) Überlegung: Damit in zwei Jahren 129€ zur Verfügung stehen, muss Herr Schlau heute bei 3% Zinsen jenen Betrag einzahlen, der in zwei Jahren auf 129€ angewachsen ist. Es gilt: 129 = K0 · 1,03 2 , d.h. K0=121,59€. Elektromax ist daher günstiger!
b) Den gesuchten Zinssatz erhält man aus der Formel 129= 119,9 · q2 , d.h. q=1,03725 und damit wäre das Versandhausangebot ab einem Zinssatz von mehr als 3,72% günstiger!
3) a) Die folgende Tabelle zeigt den Tilgungsplan für die ersten 4 Vierteljahre:
| Gesamtschuld |
2.000,00 € |
||||
| Zahlung Vierteljahr |
200,00 € |
||||
| Zinsatz |
1,75% |
||||
| Vierteljahr |
Betrag Beginn |
Zinsen |
Zahlung |
Tilgungsanteil |
Betrag Ende |
| 1 |
2.000,00 € |
35,00 € |
200,00 € |
165,00 € |
1.835,00 € |
| 2 |
1.835,00 € |
32,11 € |
200,00 € |
167,89 € |
1.667,11 € |
| 3 |
1.667,11 € |
29,17 € |
200,00 € |
170,83 € |
1.496,29 € |
| 4 |
1.496,29 € |
26,19 € |
200,00 € |
173,81 € |
1.322,47 € |
b) Aus
der Restschuldgleichung 
berechnet
man mit q=1+ 0,07/4 und G=2000€ sowie r=200€ die Gleichung:
und
nach Einsetzen: 
. Für
t erhält man 11,088 Vierteljahre, d.h. 3 3/4 Jahre.
c) Die Restschuld nach der vorletzten Zahlung ist R11= 17,55€. Im letzten Vierteljahr sind dafür noch 0,31€ Zinsen zu bezahlen, insgesamt daher 17,86€. Der Gesamtaufwand für den Kredit beträgt daher: 11 · 200€ + 17,86€ = 2217,86€. Die folgende Graphik veranschaulicht den Vorgang der Rückzahlung:
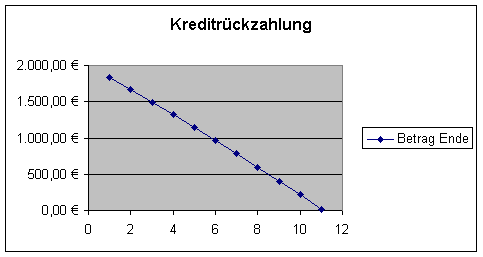
4) a) Aus der Gleichung: K6 = K0 · e – a · 6 berechnet man mit den gegebenen Werten ln(0,3)= - 6a und daraus a=0,20066. Durch Umrechnen in das Wachstumsmodell Kt = K0 · q t erhält man e –a = q = 0,818188, d.h. pro Stunde werden ca. 18,18% abgebaut.
b) Für die Halbwertszeit berechnet man 3,4543 Stunden.
