4. Schularbeit

6C                                                                                                                             21. 4. 2004

1) Am Eröffnungstag des Streichelzoos „Meck&Miau“ befanden sich 93 Meerschweinchen in einem Gehege. Ein Jahr später waren es bereits 115 Meerschweinchen.

a) Wieviele Meerschweinchen werden es am Tag des 5 jährigen (10 jährigen) Jubiläums sein, wenn man annimmt, dass der Bestand linear wächst? Formuliere ein entsprechendes Wachstumsmodell!

b) Wieviele Meerschweinchen werden es am Tag des 10 jährigen Jubiläums sein, wenn man Wachstum mit konstanten prozentuellen Zuwachsraten annimmt. Formuliere auch hier ein entsprechendes Wachstumsmodell! Wie realistisch sind die Annahmen?

c) Skizziere sowohl die lineare als auch die prozentuelle Entwicklung in einer Graphik!

d) Schätze durch „Probieren“ die Zeit, in der sich die Anzahl der Meerschweinchen bei Annahme konstanter prozentueller Zuwachsraten verdoppelt!

2) Um die Funktion der Bauchspeicheldrüse zu testen, wird ein bestimmter Farbstoff in sie eingespritzt und dessen Ausscheiden gemessen. Eine gesunde Bauchspeicheldrüse scheidet pro Minute etwa 4% des noch vorhandenen Farbstoffes aus. Bei einer Untersuchung werden einem Patienten 0,2 Gramm des Farbstoffes injiziert. Nach 30 Minuten sind noch 0,09 Gramm des Farbstoffes in seiner Bauchspeicheldrüse vorhanden. a) Bestimme die Modellgleichung für den Abbau des Farbstoffes! Funktioniert seine Bauchspeicheldrüse normal?

b) Welche Menge darf man einem gesunden Patienten höchstens injizieren, wenn nach einer Stunde nur noch 0,1 Gramm des Farbstoffes vorhanden sein dürfen?

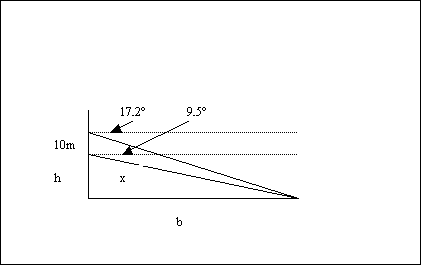
3) Am Ufer eines Flusses steht ein Turm mit zwei lotrecht übereinanderliegenden Fenstern, deren Mitten 10m voneinander entfernt sind. Von den beiden Fenstern aus erblickt man das jenseitige Ufer unter den Tiefenwinkeln  a=9,5°  und  b= 17,2° .

a)      Wie breit ist der Fluss an dieser Stelle?

b)      Wie hoch liegt das obere Fenster über dem Fluss?

c)      Unter welchem Tiefenwinkel sieht man vom oberen Fenster aus ein Boot, das sich in der Mitte des Flusses befindet?

[1) a) 2P. b) 2P. c) 2P. d) 2P. 2) a) 3P. b) 2P. 3) a) 3P. b) 2P. c) 2P.]

Lösungen:

1)       a) Aus den vorgegebenen Werten ermittelt man eine absoluten Zuwachs von 22 Meerschweinchen pro Jahr. Das entsprechende lineare Wachstumsmodell lautet somit M_t= M₀ + 22 ∙ t mit M₀=93. Man erhält demnach für M₅=203 und M₁₀=313.

b) Aus den vorgegebenen Werten berechnet man den Wachstumsfaktor q als q= ¹¹⁵/₉₃ =1,2366. Das entsprechende Wachstumsmodell lautet daher M_t= M₀  ∙ q^t mit M₀= 93 und q=1,2366. Man erhält aus dieser Gleichung für M₅=268,9 ≈ 269 und für M₁₀=777,4 ≈ 777 Meerschweinchen.

c)  Für die Entwicklung der Anzahl von Meerschweinchen kann man folgendes Bild zeichnen:

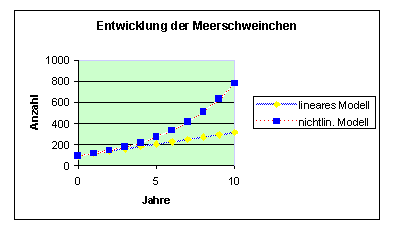
d) Da uns noch keine logarithmischen Berechnungen zur Verfügung stehen, schätzen wir die Verdopplungszeit durch systematisches Probieren. Man erhält sehr rasch t ≈ 3 ¹/₄ Jahre.

2)       a) Aus der vorgegebenen Abbaurate von 4% berechnet man den Abnahmefaktor q=0,96. Das entsprechende  Abnahmengesetz lautet daher: F_t=F₀ ∙ 0,96 ^t . Setzt man für F₀=0,2 Gramm ein, erhält man für t=30:

F₃₀= 0,058. Dieser Wert ist deutlich geringer als der beim Patienten gemessene Wert. Man muss davon ausgehen, dass die Bauchspeicheldrüse nicht ordnungsgemäß funktioniert.

b) Für einen gesunden Menschen soll gelten: M₆₀ = M₀ ∙ 0,96 ^t mit M₆₀= 0,1 und t=60. Daraus berechnet man die Anfangsmenge M₀=1,158 Gramm.

3) Man berechnet für x mit dem Sinussatz x=71,29m, danach mit dem Sinus im rechtwinkligen Dreieck h=11,76m. Zum Schluss die Breite des Flusses b=70,31m. Für den Tiefenwinkel zum Boot erhält man ε=31,4026°. (Achtung: Gesucht ist der Tiefenwinkel und nicht der Winkel im unteren rechtwinkligen Dreieck!)

Skizze: