- Schularbeit
6C 2. 12. 2003
1) a) Bestimme die Normalvektorform der Gleichung einer Ebene E, die durch A (2, 4, 4) geht und die Gerade g: X=(-1, 6, 3)+s×(1, 2, -1) enthält! Welche spezielle Lage hat diese Ebene?
b) Bestimme die gegenseitige Lage von E und der Geraden h: X=(1, -1, 2) + t×(2, 4, -1)!
c) Spiegle den Punkt P(3, 8, 12) an der Ebene E und berechne die Koordinaten des gespiegelten Punktes P1!
2) Bestimme die gegenseitige Lage der beiden Ebenen E1: 3x + 2y – z = 4 und E2. E2 ist durch die beiden parallelen Geraden g: X=(1, 0, 0) + s×(2, 1, -1) und h: X=(-4, -3, 2) + t×(2, 1, -1) festgelegt!
3) a) Zeige, dass das Dreieck A(1, -1, 2), B(4, -1, 1) C(4, -4, 2) gleichschenklig ist!
b) Dieses Dreieck bildet mit S(6, 4, 17) eine dreiseitige Pyramide. Zeige, dass S genau senkrecht über A liegt!
4) Vereinfache die folgenden Terme, beachte dabei die Rechenregeln für Potenzen!
a)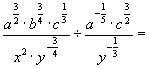 
b)
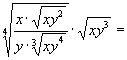
[1)a) 3P. b)3P. c) 2P. 2) 4P. 3) a) 2P. b) 2P. 4) a)3P. b)3P.]
Lösungen:
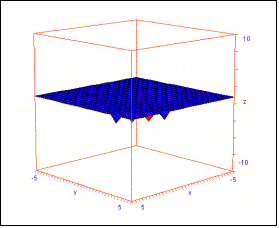1) a) Ein zweiter Richtungsvektor
ergibt sich aus den beiden gegebenen Punkten: b=(-3, 2, -1). Damit lautet
die Ebene E:y+2z=12. E liegt parallel zur x-Achse!
b) Beim Schneiden von Ebene und Gerade erhält man t = 9/2 und damit den Schnittpunkt S(10, 17, -5/2).
c) Zunächst berechnet man den Fußpunkt F durch Schneiden der Ebene E mit der Geraden h.
Man erhält F( 3, 4, 4) und für P1(3, 0, -4).
2) Auch hier erhält man den Richtungsvektor aus den beiden Punkten der parallelen Geraden,
nämlich v=(-5, -3, 2).
Der Normalvektor der Ebene ist daher n=(1, -1, 1). Die Ebenengleichung lautet daher: E: x – y + z = 1. Eliminiert man z und setzt anschließend x=t, erhält man als Schnittgerade g: X=(0, 5, 6) + t×(1, -4, -5).
3) a) Die beiden Vektoren AB und BC haben dieselbe Länge!
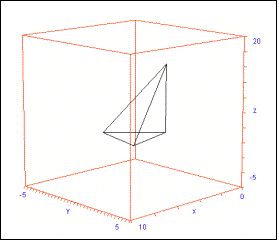b) Die Gleichung der
Ebene durch A, B, und C lautet E: x + y + 3z = 6 . Wegen AS=(5, 5, 15) und
nE
// AS stimmt es, dass S genau über A liegt! (Graphik!)
3) a) 
b) 